公式 母標準偏差を σ ,標本平均を X ― ,標本の大きさを n とすると、母平均 μ の信頼区間を求める式は、 X ― − z ⋅ σ n ≦ μ ≦ X ― z ⋅ σ n ただし、信頼度が c % のとき z は、右図を標準正規分布の確率分布図として、図中の z 0 の値。 特に 信頼
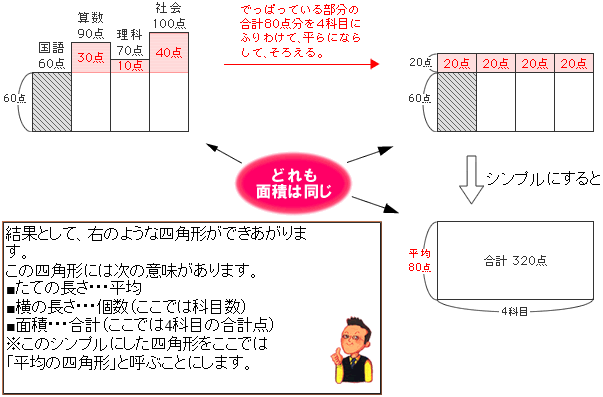
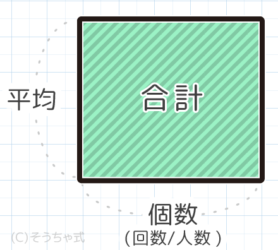
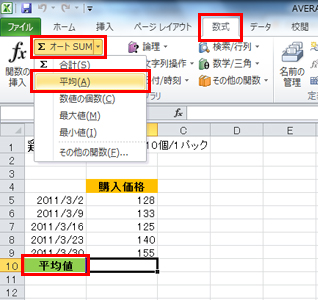
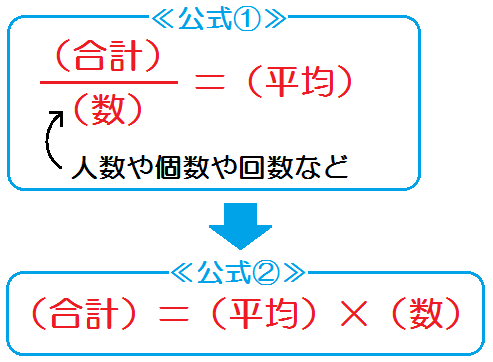
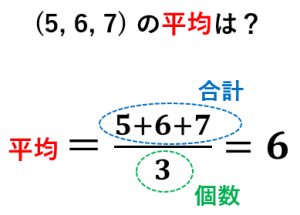
平均の公式-平均値qの公式を下記に示します。 Σaはデータの値の合計、Σnはデータの個数の合計(総数)です。 平均値の求め方ですが、まずはデータの値を合計します。次にデータの個数の合計で割ります。 平均値と中央値との関係 平均値と中央値の違いを下記に よって、平均の速度を求める公式は次のようになります。 \begin{align} 平均の速度=\frac{\text{変位}\Delta{x}}{\text{かかった時間}\Delta{t}} \end{align} ちなみに山手線で東京駅を出発し、1周して東京駅に戻ってきたとき平均の速度は0です。
平均の公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  |  |
 |  |  |
「平均の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 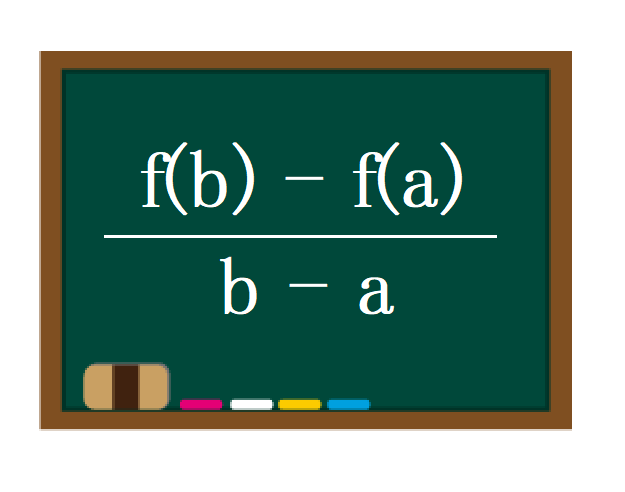 |
 |  |  |
 |  |  |
 |  | |
「平均の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | 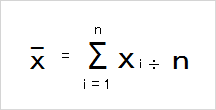 | |
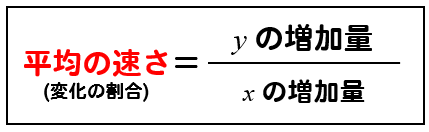 |  | |
「平均の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「平均の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
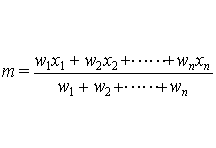 |  | |
「平均の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「平均の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「平均の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 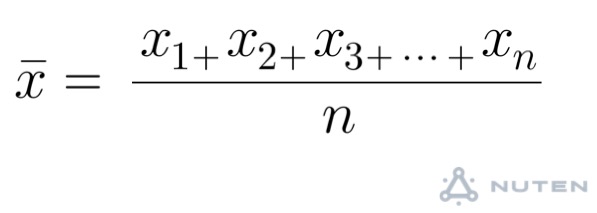 |  |
 |  | |
 |  |  |
「平均の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | 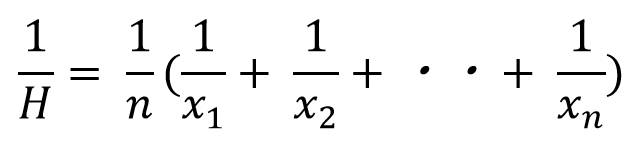 |  |
 |  |
平均値の変換公式とその証明 今、あるデータxとyがy=axb という関係式で結ばれているとします。 この時、xの平均値をyで表すにはどのようにすればよいでしょうか? 平均値の変換公式 \(\overline{y}=a\overline{x}b\)・・・(1) 確率変数の和の分散の導出方法 次に,分散を求めていきます. こちらも先程の平均と同じように,周辺分布の分散をそれぞれ , ,同時分布から求められる分散を , とします. 確率変数の和の分散は,分散の公式を使用すると以下のようにして求められ
Incoming Term: 平均の公式,




0 件のコメント:
コメントを投稿